Difference between revisions of "Phasors Review/Calculations Example"
(→$$\omega$$=80000 rad/s) |
|||
| (11 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
Assume you have an independent voltage source connected to a series combination of an inductor and a resistor and you want to find the current through the mesh (labeled as the current through the inductor). Using phasor analysis, you can get the transfer function:<center><math>\begin{align*}\mathbb{H}(j\omega)&=\frac{\mathbb{I}_{\omega}}{\mathbb{V}_{\omega}}=\frac{1}{j\omega L + R}\end{align*}</math></center>where $$\mathbb{V}_{\omega}$$ represents the magnitude and phase of a single-frequency sinusoid of the voltage source at frequency $$\omega$$ and $$\mathbb{I}_{\omega}$$ represents the magnitude and phase of a single-frequency sinusoid of the steady state current at frequency $$\omega$$. | Assume you have an independent voltage source connected to a series combination of an inductor and a resistor and you want to find the current through the mesh (labeled as the current through the inductor). Using phasor analysis, you can get the transfer function:<center><math>\begin{align*}\mathbb{H}(j\omega)&=\frac{\mathbb{I}_{\omega}}{\mathbb{V}_{\omega}}=\frac{1}{j\omega L + R}\end{align*}</math></center>where $$\mathbb{V}_{\omega}$$ represents the magnitude and phase of a single-frequency sinusoid of the voltage source at frequency $$\omega$$ and $$\mathbb{I}_{\omega}$$ represents the magnitude and phase of a single-frequency sinusoid of the steady state current at frequency $$\omega$$. | ||
== AC Steady State Calculations == | == AC Steady State Calculations == | ||
| − | If you further assume that the circuit has been in place for a long time and under the influence of one (or more) single-frequency sinusoidal voltages, you can find the AC steady state current using phasor analysis by noting that: <center><math>\begin{align*}\mathbb{I}_{\omega}=\mathbb{V}_{\omega}\,\mathbb{H}(j\omega)\end{align*}</math></center> | + | If you further assume that the circuit has been in place for a long time and under the influence of one (or more) single-frequency sinusoidal voltages, you can find the AC steady state current using phasor analysis by noting that: <center><math>\begin{align*}\mathbb{I}_{\omega}=\mathbb{V}_{\omega}\,\mathbb{H}(j\omega)\end{align*}</math></center> |
| − | Assume for this particular circuit that $$R=1$$ k$$\Omega$$ | + | Assume for this particular circuit that $$R=1$$ k$$\Omega$$ and $$L=20$$ mH, meaning:<center><math>\begin{align*}\mathbb{H}(j\omega)&=\frac{1}{j\omega\,0.02 + 1000}\end{align*}</math></center> |
| + | |||
| + | Further assume that:<center><math>v(t)=2+3\cos(40000t+56^{\circ})+7\sin(80000t-9^{\circ})~\mbox{V}</math></center> | ||
=== Convert to Cosine === | === Convert to Cosine === | ||
Typically, phasor analysis is performed using cosine. You '''could''' start and finish with sine but it is more common to first convert sine to cosine using the relationship $$\sin(\theta)=\cos(\theta-90^{\circ})$$. Given that, <center><math>v(t)=2+3\cos(40000t+56^{\circ})+7\cos(80000t-99^{\circ})~\mbox{V}</math></center> | Typically, phasor analysis is performed using cosine. You '''could''' start and finish with sine but it is more common to first convert sine to cosine using the relationship $$\sin(\theta)=\cos(\theta-90^{\circ})$$. Given that, <center><math>v(t)=2+3\cos(40000t+56^{\circ})+7\cos(80000t-99^{\circ})~\mbox{V}</math></center> | ||
| Line 27: | Line 29: | ||
==== Calculator Preparation ==== | ==== Calculator Preparation ==== | ||
You will need to make sure your calculator is in the right mode to do complex calculations and to display them in a useful way. Also, it will be handy to store the conversion from degrees to radians as a constant in the calculator because you will need to use that every time you want to calculate a complex number using a magnitude and an angle in degrees - the calculator will only accept radians! See [[Calculator_Tips#Initial_Setup]] and follow the steps to get your calculator ready. | You will need to make sure your calculator is in the right mode to do complex calculations and to display them in a useful way. Also, it will be handy to store the conversion from degrees to radians as a constant in the calculator because you will need to use that every time you want to calculate a complex number using a magnitude and an angle in degrees - the calculator will only accept radians! See [[Calculator_Tips#Initial_Setup]] and follow the steps to get your calculator ready. | ||
| + | ==== Finding Transfer Function and Current Phasor ==== | ||
| + | ===== $$\omega$$=0 rad/s ===== | ||
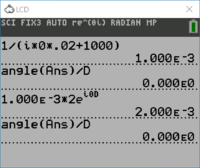
| + | [[File:TI84_filter_0.PNG|200px|thumb|right|Calculations when $$\omega=0$$ rad/s.]] | ||
| + | For the case where $$\omega=0$$, you should not even need a calculator to figure out that $$\mathbb{H}(j\omega)=\frac{1}{1000}=0.001$$. But if you wanted to see what this might look like, check out the figure on the right. The example goes through the process of calculating the transfer function and then extracting the angle in degrees from it. Since the transfer function is a positive real value here, the angle is $$0^{\circ}$$. Once you have that, you will multiply the transfer function by the input phasor. Again, since this is simply 2, you can do this without a calculator, but the process is shown at right in a very formal way. You can up-arrow to select the transfer function result and then hit ENTER to repeat it in your current calculation. You can then formally enter 2 as $$2\angle0^{\circ}$$ (you could also just use 2 here). Next, if you want to get the angle of the output phasor, you can use the <code>angle</code> command. Finally, you can use the output phasor at 0 rad/s to get the output current at 0 rad/s. The table now looks like:<center><math>\begin{array}{|c|c|c|c|c|}\hline | ||
| + | \omega & \mathbb{V}_{\omega} & \mathbb{H}(j\omega) & \mathbb{I}_{\omega}=\mathbb{V}_{\omega}\,\mathbb{H}(j\omega) & i(t)=I\,\cos(\omega t+\phi_I)\\ \hline | ||
| + | 0 & 2\angle 0^{\circ} & 1\times10^{-3}\angle0^{\circ} & 2\times10^{-3}\angle0^{\circ} & 2\times10^{-3} \\ \hline | ||
| + | 40000 & 3\angle 56^{\circ} & ~ & ~ & \\ \hline | ||
| + | 80000 & 7\angle-{99^{\circ}} & ~ & ~ & \\ \hline | ||
| + | \end{array}</math></center> | ||
| + | |||
| + | ===== $$\omega$$=40000 rad/s===== | ||
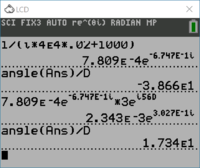
| + | [[File:TI84_filter_40k.PNG|200px|thumb|right|Calculations when $$\omega=40$$ krad/s.]] | ||
| + | You will now follow the same process above for $$\omega$$=40000 rad/s. If you typed the commands in above, you can use the up-arrow to go back through previous commands, enter to repeat the command, and then use the left and right arrows to place the cursor at the point in the command where you want to make a change. Note that the default case is to overwrite characters if you type new ones; if you want to insert characters instead, type <code>2ND, INS</code> (above the <code>DEL</code>) key. The four lines you need to figure out the $$\omega=40$$ krad/s values are shown at right. The table is now: | ||
| + | <center><math>\begin{array}{|c|c|c|c|c|}\hline | ||
| + | \omega & \mathbb{V}_{\omega} & \mathbb{H}(j\omega) & \mathbb{I}_{\omega}=\mathbb{V}_{\omega}\,\mathbb{H}(j\omega) & i(t)=I\,\cos(\omega t+\phi_I)\\ \hline | ||
| + | 0 & 2\angle 0^{\circ} & 1\times10^{-3}\angle0^{\circ} & 2\times10^{-3}\angle0^{\circ} & 2\times10^{-3} \\ \hline | ||
| + | 40000 & 3\angle 56^{\circ} & 7.809\times10^{-4}\angle-38.66^{\circ} & 2.343\times10^{-3}\angle17.43^{\circ} & 2.343\times10^{-3}\,\cos(40000t+17.43^{\circ})\\ \hline | ||
| + | 80000 & 7\angle-{99^{\circ}} & ~ & ~ & \\ \hline | ||
| + | \end{array}</math></center> | ||
| + | |||
| + | ===== $$\omega$$=80000 rad/s===== | ||
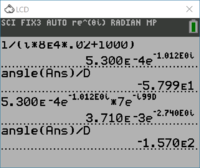
| + | [[File:TI84_filter_80k.PNG|200px|thumb|right|Calculations when $$\omega=80$$ krad/s.]] | ||
| + | Finally, you will follow the same process above for $$\omega$$=80000 rad/s. Use the arrow keys to select and repeat commands as needed. The four lines you need to figure out the $$\omega=80$$ krad/s values are shown at right. The table is now: | ||
| + | <center><math>\begin{array}{|c|c|c|c|c|}\hline | ||
| + | \omega & \mathbb{V}_{\omega} & \mathbb{H}(j\omega) & \mathbb{I}_{\omega}=\mathbb{V}_{\omega}\,\mathbb{H}(j\omega) & i(t)=I\,\cos(\omega t+\phi_I)\\ \hline | ||
| + | 0 & 2\angle 0^{\circ} & 1\times10^{-3}\angle0^{\circ} & 2\times10^{-3}\angle0^{\circ} & 2\times10^{-3} \\ \hline | ||
| + | 40000 & 3\angle 56^{\circ} & 7.809\times10^{-4}\angle-38.66^{\circ} & 2.343\times10^{-3}\angle17.43^{\circ} & 2.343\times10^{-3}\,\cos(40000t+17.43^{\circ})\\ \hline | ||
| + | 80000 & 7\angle-{99^{\circ}} & 5.300\times10^{-4}\angle-57.99^{\circ} & 3.710\times10^{-3}\angle1-157.0^{\circ} & 3.710\times10^{-3}\,\cos(80000t-157.0^{\circ}) \\ \hline | ||
| + | \end{array}</math></center> | ||
| + | |||
| + | === Putting it All Together === | ||
| + | The last step is simply to add all the items in the last column together to get:<center><math> | ||
| + | i(t)=2+2.343\,\cos(40000t+17.43^{\circ})+3.710\,\cos(80000t-157.0^{\circ})\mbox{ mA} | ||
| + | </math></center> | ||
Latest revision as of 02:36, 16 March 2024
Contents
Introduction
Assume you have an independent voltage source connected to a series combination of an inductor and a resistor and you want to find the current through the mesh (labeled as the current through the inductor). Using phasor analysis, you can get the transfer function:
where $$\mathbb{V}_{\omega}$$ represents the magnitude and phase of a single-frequency sinusoid of the voltage source at frequency $$\omega$$ and $$\mathbb{I}_{\omega}$$ represents the magnitude and phase of a single-frequency sinusoid of the steady state current at frequency $$\omega$$.
AC Steady State Calculations
If you further assume that the circuit has been in place for a long time and under the influence of one (or more) single-frequency sinusoidal voltages, you can find the AC steady state current using phasor analysis by noting that:
Assume for this particular circuit that $$R=1$$ k$$\Omega$$ and $$L=20$$ mH, meaning:
Further assume that:
Convert to Cosine
Typically, phasor analysis is performed using cosine. You could start and finish with sine but it is more common to first convert sine to cosine using the relationship $$\sin(\theta)=\cos(\theta-90^{\circ})$$. Given that,
Make a Table
Now that you have all the sinusoids in terms of cosine, you can split the voltages into their individual frequencies. You will generally need to keep track of the frequency, the voltage phasor at that frequency, the value of the transfer function at that frequency, the current phasor at that frequency (which will be the product of the voltage phasor and the transfer function), and finally the time-domain current represented by that phasor. Start the table as follows:
Fill in the Voltage Phasors
Once you have the table set up, you can put in the magnitudes and phases for the voltage phasors at each frequency. For the signal given above, this means:
Calculate the Transfer Function and Output Phasor Values
Next you will need to find values for $$\mathbb{H}(j\omega)$$ and $$\mathbb{I}_{\omega}$$. The following steps assume you are using some form of TI-84+ calculator.
Calculator Preparation
You will need to make sure your calculator is in the right mode to do complex calculations and to display them in a useful way. Also, it will be handy to store the conversion from degrees to radians as a constant in the calculator because you will need to use that every time you want to calculate a complex number using a magnitude and an angle in degrees - the calculator will only accept radians! See Calculator_Tips#Initial_Setup and follow the steps to get your calculator ready.
Finding Transfer Function and Current Phasor
$$\omega$$=0 rad/s
For the case where $$\omega=0$$, you should not even need a calculator to figure out that $$\mathbb{H}(j\omega)=\frac{1}{1000}=0.001$$. But if you wanted to see what this might look like, check out the figure on the right. The example goes through the process of calculating the transfer function and then extracting the angle in degrees from it. Since the transfer function is a positive real value here, the angle is $$0^{\circ}$$. Once you have that, you will multiply the transfer function by the input phasor. Again, since this is simply 2, you can do this without a calculator, but the process is shown at right in a very formal way. You can up-arrow to select the transfer function result and then hit ENTER to repeat it in your current calculation. You can then formally enter 2 as $$2\angle0^{\circ}$$ (you could also just use 2 here). Next, if you want to get the angle of the output phasor, you can use the angle command. Finally, you can use the output phasor at 0 rad/s to get the output current at 0 rad/s. The table now looks like:
$$\omega$$=40000 rad/s
You will now follow the same process above for $$\omega$$=40000 rad/s. If you typed the commands in above, you can use the up-arrow to go back through previous commands, enter to repeat the command, and then use the left and right arrows to place the cursor at the point in the command where you want to make a change. Note that the default case is to overwrite characters if you type new ones; if you want to insert characters instead, type 2ND, INS (above the DEL) key. The four lines you need to figure out the $$\omega=40$$ krad/s values are shown at right. The table is now:
$$\omega$$=80000 rad/s
Finally, you will follow the same process above for $$\omega$$=80000 rad/s. Use the arrow keys to select and repeat commands as needed. The four lines you need to figure out the $$\omega=80$$ krad/s values are shown at right. The table is now:
Putting it All Together
The last step is simply to add all the items in the last column together to get: